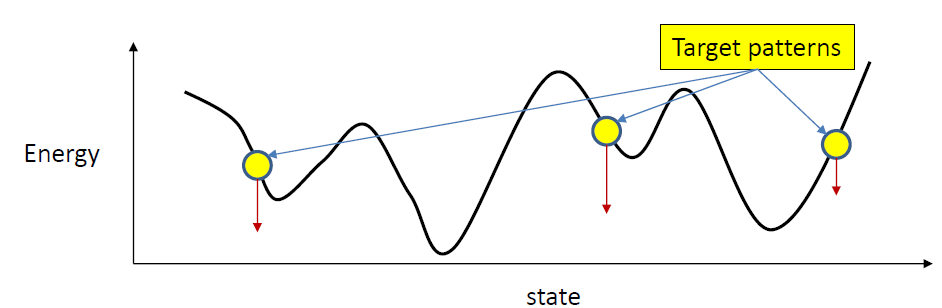
Training hopfield nets
Geometric approach
Behavior of with is identical to behavior with
- Energy landscape only differs by an additive constant
- Gradients and location of minima remain same (Have the same eigen vectors)
Sine :
We use for analyze
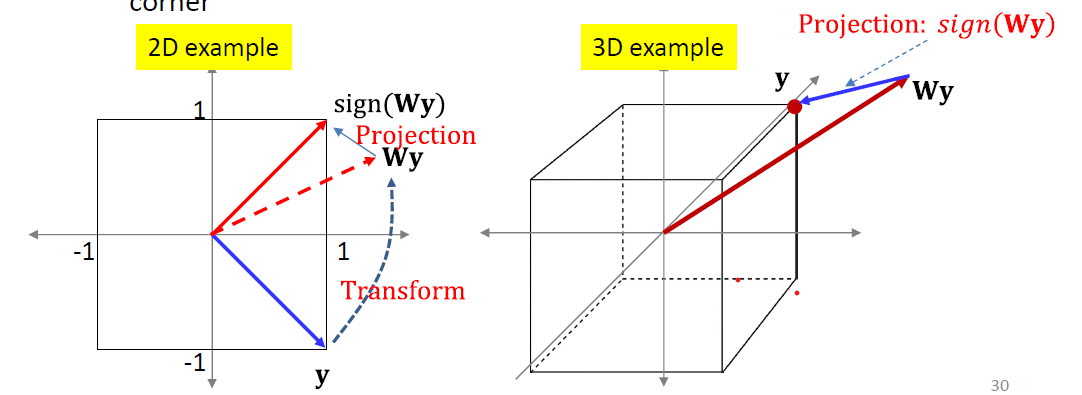
A pattern is stored if:
- for all target patterns
Training: Design such that this holds
Simple solution: is an Eigenvector of
Storing k orthogonal patterns
- Let
- are positive
- for this is exactly the Hebbian rule
- Any pattern can be written as
- All patterns are stable
- Remembers everything
- Completely useless network
- Even if we store fewer than patterns
- Let
- are orthogonal to
- Problem arise because eigen values are all 1.0
- Ensures stationarity of vectors in the subspace
- All stored patterns are equally important
General (nonorthogonal) vectors
- The maximum number of stationary patterns is actually exponential in (McElice and Posner, 84’)
- For a specific set of patterns, we can always build a network for which all patterns are stable provided
- But this may come with many “parasitic” memories
Optimization
- Energy function
- This must be maximally low for target patterns
- Must be maximally high for all other patterns
- So that they are unstable and evolve into one of the target patterns
- Estimate such that
- is minimized for
- is maximized for all other
- Minimize total energy of target patterns
- However, might also pull all the neighborhood states down
- Maximize the total energy of all non-target patterns
- Simple gradient descent
- minimize the energy at target patterns
- raise all non-target patterns
- Do we need to raise everything?
Raise negative class
- Focus on raising the valleys
- If you raise every valley, eventually they’ll all move up above the target patterns, and many will even vanish
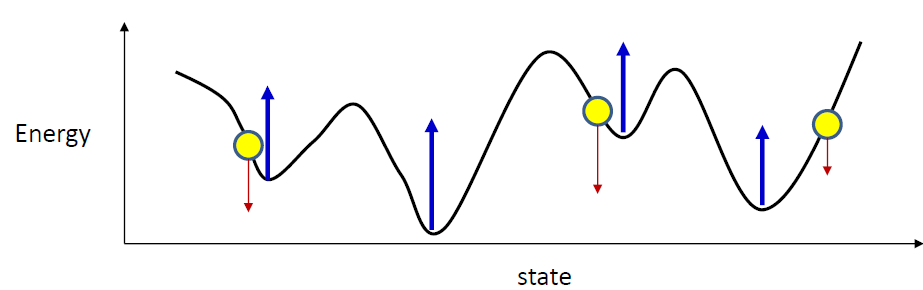
- How do you identify the valleys for the current ?
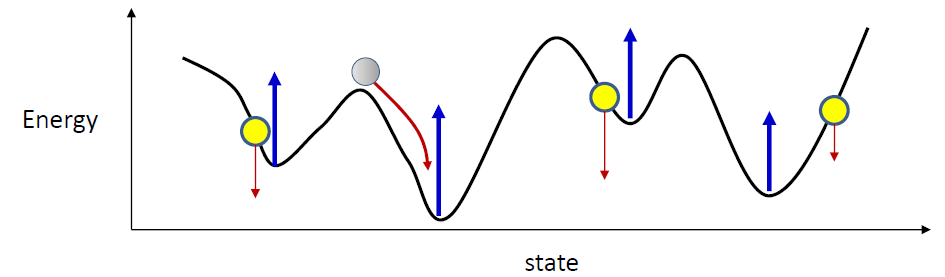
- Initialize the network randomly and let it evolve
- It will settle in a valley

- Should we randomly sample valleys?
- Are all valleys equally important?
- Major requirement: memories must be stable
- They must be broad valleys
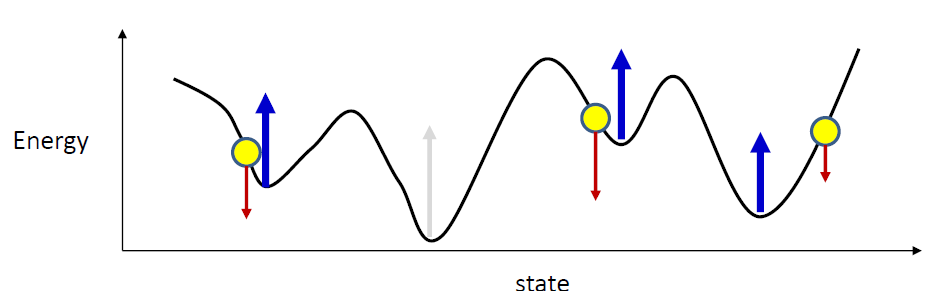
- Solution: initialize the network at valid memories and let it evolve
- It will settle in a valley
- If this is not the target pattern, raise it
- What if there’s another target pattern downvalley
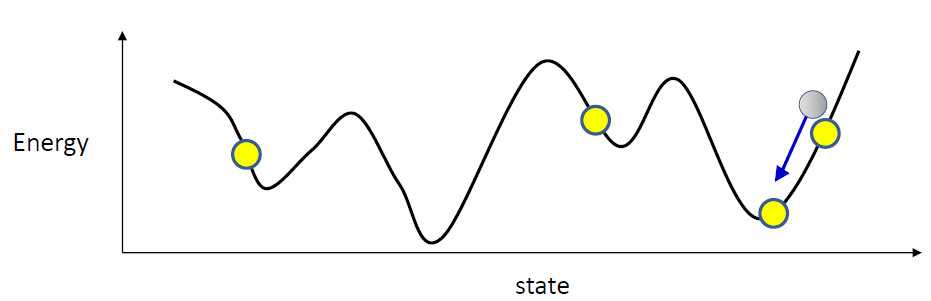
- no need to raise the entire surface, or even every valley
- Raise the neighborhood of each target memory

Storing more than N patterns
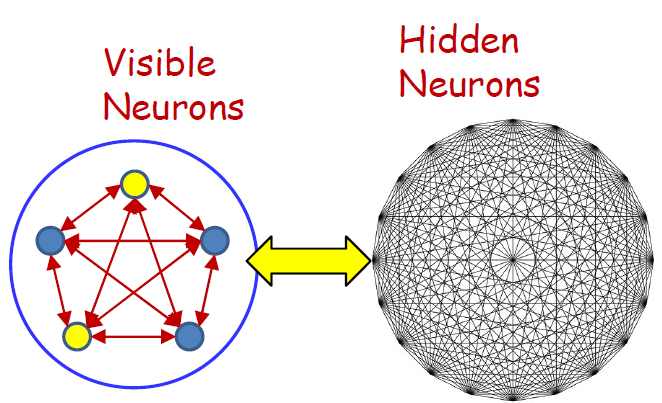
- Visible neurons
- The neurons that store the actual patterns of interest
- Hidden neurons
- The neurons that only serve to increase the capacity but whose actual values are not important
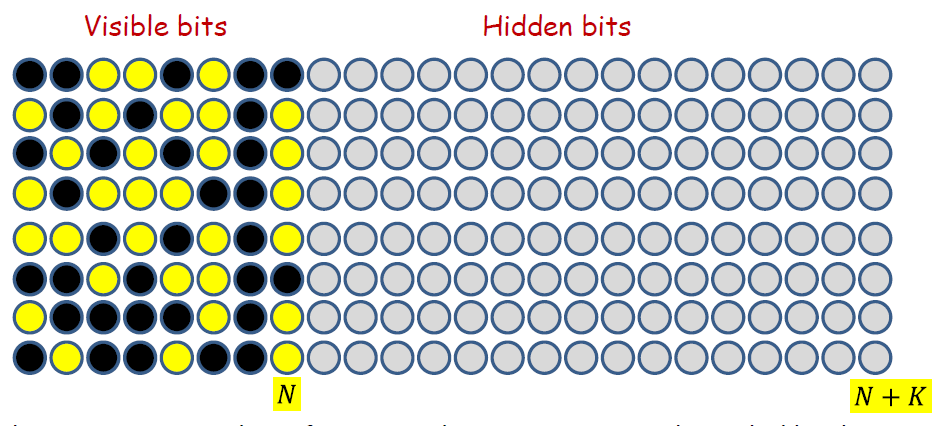
- The maximum number of patterns the net can store is bounded by the width of the patterns..
- So lets pad the patterns with “don’t care” bits
- The new width of the patterns is
- Now we can store patterns!
- Taking advantage of don’t care bits
- Simple random setting of don’t care bits, and using the usual training and recall strategies for Hopfield nets should work
- However, to exploit it properly, it helps to view the Hopfield net differently: as a probabilistic machine
A probabilistic interpretation
- For binary y the energy of a pattern is the analog of the negative log likelihood of a Boltzmann distribution
- Minimizing energy maximizes log likelihood
Boltzmann Distribution
- is the Boltzmann constant, is the temperature of the system
- Optimizing
- Simple gradient descent
- more importance to more frequently presented memories
- more importance to more attractive spurious memories
- Looks like an expectation
- The behavior of the Hopfield net is analogous to annealed dynamics of a spin glass characterized by a Boltzmann distribution